|
本文介绍拉马努金的一个神奇公式: 若 \begin{aligned} \frac{1+53x+9x^2}{1-82x-82x^2+x^3}&=\sum_{n=0}^\infty a_n x^n \\ \frac{2-26x-12x^2}{1-82x-82x^2+x^3}&= \sum_{n=0}^\infty b_n x^n \\ \frac{2+8x-10x^2}{1-82x-82x^2+x^3}&=\sum_{n=0}^\infty c_n x^n \end{aligned}\\ 则对任何 n\geq0 ,有 a_n^3+b_n^3 = c_n^3 + (-1)^n\\ 例如,当 0 \leq\ n \leq 6 时,具体的数值是: a_{n}=1, 135, 11161, 926271, 76869289, 6379224759, 529398785665 b_{n}=2, 138, 11468, 951690, 78978818, 6554290188, 543927106802 c_{n}=2, 172, 14258, 1183258, 98196140, 8149096378, 676276803218 可以验证: 1^3+2^3=2^3+(-1)^0 135^3+138^3=172^3+(-1)^1 11161^3+11468^3=14258^3+(-1)^2 926271^3+951690^3=1183258^3+(-1)^3 76869289^3+78978818^3=98196140^3+(-1)^4 等等。 很多看过这个公式的数学家都会提出这样的疑问:拉马努金是如何想到这个公式的?好几篇关于这个问题的文献,都用了 an amazing identity of Ramanujan 来形容。 近年来,受拉马努金的这个公式的启发,数学家们对等幂和问题的整数解也作出了类似的公式。 一、拉马努金的原始手迹以下是拉马努金这个神奇公式的原始手迹: 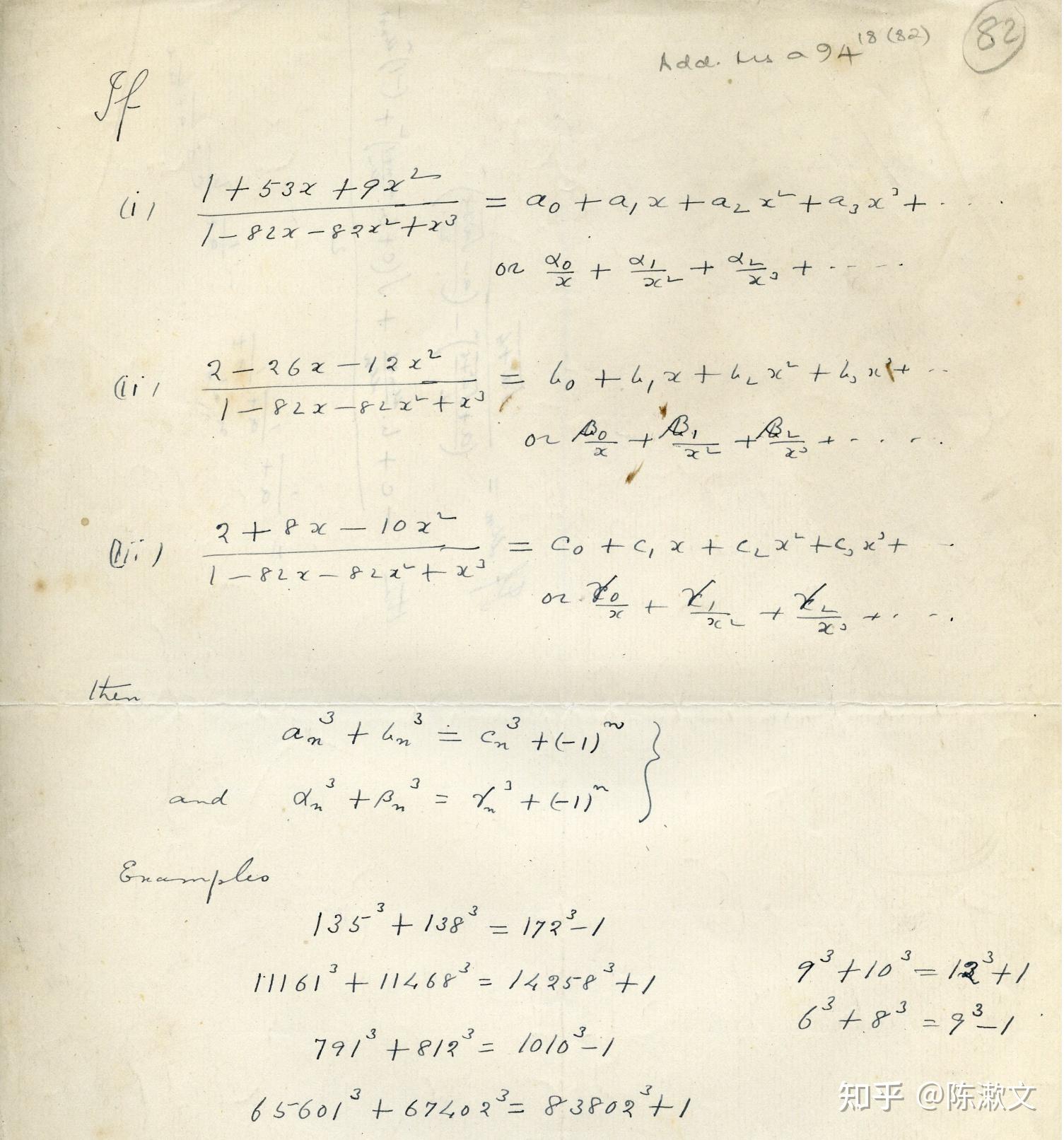 上图出处:[1] THE 1729 K3 SURFACE 这个公式也被整理在: [2]《Ramanujan's Lost Notebook(Part IV)》中,第199-205页。(该书的中国大陆授权版本,由哈尔滨工业大学出版社出版,共9卷,其中5卷是《拉马努金笔记》,4卷是《拉马努金遗失笔记》)。 拉马努金的上述公式,我尚未看到有中文的文献或介绍。在本文中,我暂用“拉马努金立方和公式”,是综合了以下国外链接的叫法: [3] Generalizing Ramanujan's sum of cubes identity? [4] How did people get the inspiration for the sums of cubes formula? [5] Ramanujan's Sum Identity 二、M.D.Hirschhorn 等人对拉马努金立方和公式的证明拉马努金对立方和公式只留下了上图手迹,人们一直都对拉马努金是如何想到这个公式深感疑惑,直到1995年,才出现突破。 【证明一】 1995年,新南威尔士大学的 M.D.Hirschhorn 给出了拉马努金立方和公式的第一种证明方法,并对拉马努金发现这个公式的可能思路给出了一个合理的解释。其论文链接(付费): [6] An Amazing Identity of Ramanujan 或 参看文献 [2] [5] 在该文中,M.D.Hirschhorn认为,拉马努金的思路很可能是源于他更早时发现的以下立方和参数解公式: \left( 3 a^2 +5ab - 5 b^2 \right)^3 + \left( 4 a^2 - 4ab + 6 b^2 \right)^3 + \left( 5 a^2 - 5ab -3 b^2 \right)^3=\left( 6 a^2 - 4ab + 4 b^2 \right)^3 【证明二】 其后,M.D.Hirschhorn 于1996年给出了第二种证明方法,论文链接(付费): [7] A proof in the spirit of Zeilberger of an amazing identity of Ramanujan 或 参看[2] 在该文,M.D.Hirschhorn 先把拉马努金的参数解式子变形如下: (A^2+7AB-9B^2)^3+(2A^2-4AB+12B^2)^3=(2A^2+10B^2)^3+(A^2-9AB-B^2)^3 这篇文章给出的第二种证明方法,更具普遍意义,其后人们进一步对拉马努金立方和公式作推广,也是源于此思路。 【证明三】 十年后的2006年,J. H.Han 和 M. D.Hirschhorn 给出了第三种证明方法,论文链接(免费): [8] ANOTHER LOOK AT AN AMAZING IDENTITY OF RAMANUJAN 此方法证明了拉马努金立方和公式的 \{a_n\}, \{b_n\}, \{c_n\} 可以通过特定的矩阵方程得到: \begin{array}{} \begin{bmatrix} a_n \\\ b_n \\\ c_n \end{bmatrix} & = {\begin{bmatrix} 63 & 104 & 68 \\\ 64 & 104 & 67 \\\ 80 & 131 & 85 \end{bmatrix}}^n & \cdot & \begin{bmatrix} 1 \\\ 2 \\\ 2 \end{bmatrix} \end{array}\\ 【其他立方和公式】 Tito Piezas III 在 文献 [3] 指出,拉马努金立方和公式还可以增补如下形式:若 \begin{aligned} \frac{9+53x+x^2}{1-82x-82x^2+x^3}&=\sum_{n=0}^\infty a_n x^n \\ \frac{-12-26x-2x^2}{1-82x-82x^2+x^3}&= \sum_{n=0}^\infty b_n x^n \\ \frac{-10+8x+2x^2}{1-82x-82x^2+x^3}&=\sum_{n=0}^\infty c_n x^n \end{aligned}\\ 则对任何 n\geq0 ,有 a_n^3+b_n^3 = c_n^3 + 1^n Tito Piezas III 在 文献 [3] 中,还给出了一个新的立方和公式:若 \frac{-9(417-5602x+x^2)}{-1+184899x-184899x^2+x^3}=\sum_{n=0}^\infty a_n x^n \\ \frac{8(-566-11315x+x^2)}{-1+184899x-184899x^2+x^3}=\sum_{n=0}^\infty b_n x^n \\ \frac{-6(877+6898x+x^2)}{-1+184899x-184899x^2+x^3}=\sum_{n=0}^\infty c_n x^n 则对任何 n\geq0 ,有 a_n^3+b_n^3 = c_n^3 + 1^n Derek指出,这个公式也可以由特定的矩阵方程得到: \begin{array} {} \begin{bmatrix} a_n \\\ b_n \\\ c_n \end{bmatrix} &=& {\begin{bmatrix} 156625 & 115992 & 79656 \\\ 189000 & 139969 & 96120 \\\ 219624 & 162648 & 111695 \end{bmatrix}}^n \cdot \begin{bmatrix} 3753 \\\ 4528 \\\ 5262 \end{bmatrix} \end{array}\\ 相关链接: [9] How can you verify that a 3 by 3 unimodular matrix generates an infinite number of Fermat near misses? 三、J.M.Laughlin 对拉马努金立方和公式的推广美国西切斯特大学的 J.M.Laughlin 先后于2008年、2010年及2019年发了三篇题目相同的论文《 An Identity Motivated by an Amazing Identity of Ramanujan 》,其中2008年版本现在网络上已经找不到,但我前些年保存了,似乎是预印本;2010年版本正式发布在《Fibonacci Quarterly》杂志,有点奇怪的是,J.M.Laughlin 于2019年再度在arxiv平台发布了一个注明 January 16, 2019 日期的版本: [10] An Identity Motivated by an Amazing Identity of Ramanujan (2010版) [11] An Identity Motivated by an Amazing Identity of Ramanujan (2019版) 我未发现2010年版本与2019年版本的细微差别,两个版本的内容都是把拉马努金立方和公式推广至五次方等幂和问题,但2008年版本还是有所区别,其推广的用例是七次方等幂和问题。(方法本质上是一样的,仅是例子上的差别)。在2010年版和2019年版的论文中,J.M.Laughlin 受拉马努金立方和公式的启发,给出了以下五次方等幂和问题的类似公式:  例如,由上式可得 \{a_1, b_1, c_1, d_1, e_1, f_1, p_1, q_1, r_1, s_1, t_1\} =\{461, 233, 199, 465, 237, 203, 435, 343, 439, 347, 3\} 对于 1\leq j \leq 5 均满足(461)^j + (233)^j + (199)^j + 465^j + 237^j + 203^j\\ = (435)^j + (343)^j + 439^j + 347^j + 3^j + 1^j J.M.Laughlin 指出,他的上述等幂和公式,是基于五次方等幂和问题的以下公式解:  J.M.Laughlin 所做的推广,令拉马努金立方和公式从三次方的不定方程拓展至五次方/七次方的不定方程组,结果还是很惊艳的,这一成果也被收录到前述的文献 [2],即《拉马努金遗失笔记》的第四卷中。从论文原文不难看出,J.M.Laughlin 得到上述公式所用的方法,和M.D.Hirschhorn 对拉马努金立方和公式的第二种证明方法,思路是完全相同的。 顺便一提,J.M.Laughlin 上述论文的参考文献8,就是我的等幂和问题网站的2001年版本。事实上,我正是前几年在Google学术和百度学术上搜索我的网站被引用状况时,注意到J.M.Laughlin 的文章的,从而令我第一次了解到神奇的拉马努金立方和公式。(我的网站的新版本地址:eslpower.org ) 四、KWANG-WU CHEN 对拉马努金立方和公式的推广2012年,台北市立教育大學的 Kwang-Wu Chen 在总结 M. D.Hirschhorn 和 J.M.Laughlin 所做成果的基础上,发布了以下文章: [12] Extensions of an amazing identity of Ramanujan Kwang-Wu Chen 的这篇文章,归纳整理了 M. D.Hirschhorn 和 J.M.Laughlin 的思路,指出了对拉马努金立方和公式进行推广的关键点是: 对于不定方程(或不定方程组) x_{1}^{n}+x_{2}^{n}+\cdots+x_{l}^{n}=y_{1}^{n}+y_{2}^{n}+\cdots+y_{l}^{n} ,首先需要找出如下形式的 两参数二次方公式解 x_{i} = α_{i1}p^2 + α_{i2} p q + α_{i3}q^2\\ y_{i} = β_{i1}p^2+ β_{i2} p q + β_{i3}q^2 在方法上,Kwang-Wu Chen 的论文没有太新的突破,但这篇文章写得比较具体和有条理,有助于我们理解 M. D.Hirschhorn 和 J.M.Laughlin 的那几篇论文。此外,Kwang-Wu Chen 给出以下例子,是关于 拉马努金 6-10-8 公式 以及 Hirschhorn's 3-7-5 公式的: 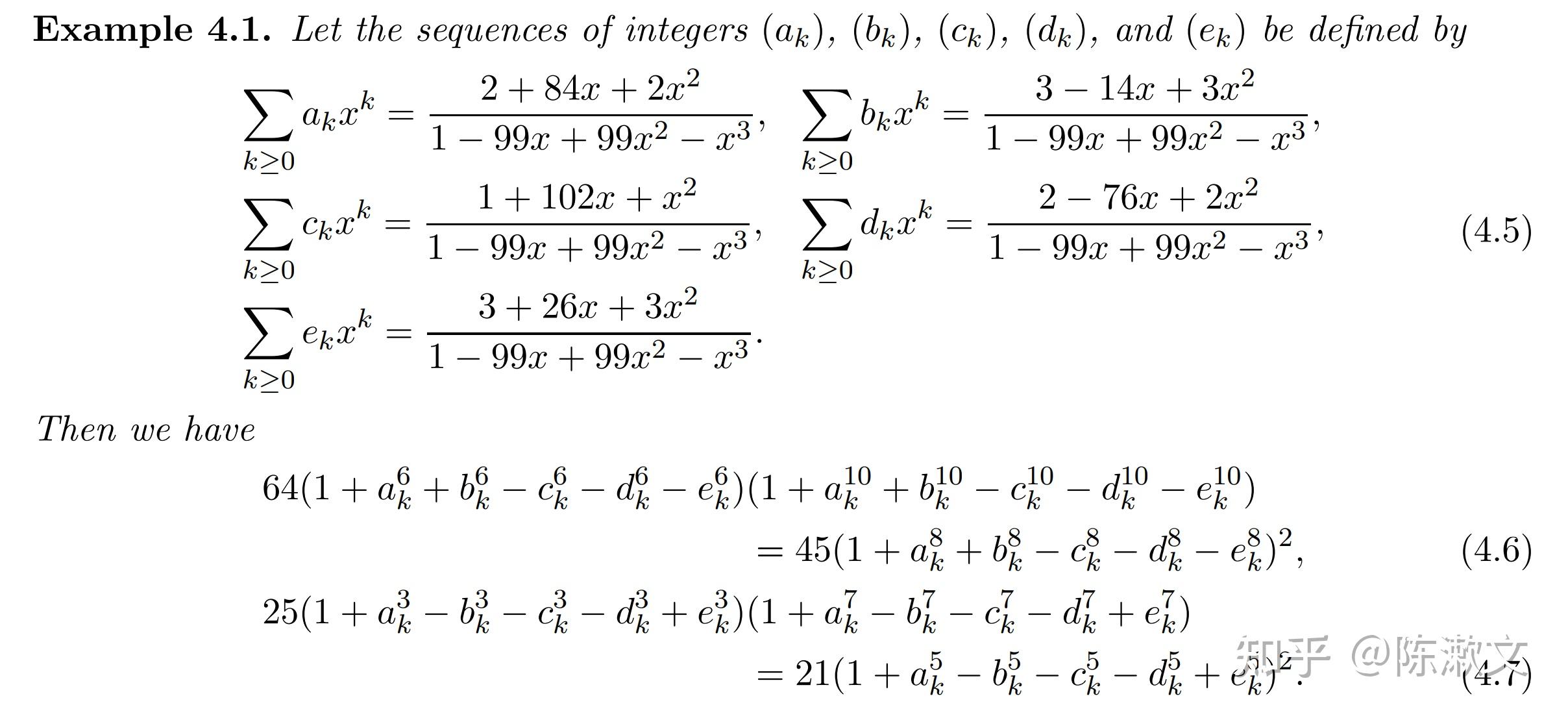 从形式上看,这两个式子是对拉马努金立方和公式的新推广;从本质上看,没有突破J.M.Laughlin 所做的工作,同样是把拉马努金立方和公式推广在等幂和问题上。对于 拉马努金 6-10-8 公式 以及 Hirschhorn's 3-7-5 公式,我曾经在前两年做过专门研究,做了更深入的推广:Identity (eslpower.org) 五、本人对拉马努金立方和公式及其推广的理解我前几年第一次看到 J.M.Laughlin 的论文时,惊讶于拉马努金立方和公式的神奇,也赞叹J.M.Laughlin 五次方等幂和公式的美妙,但当时我判断,这些公式对于等幂和问题的解决,作用不大,就没有深入探究。最近两周,我有些想法,能否通过对 J.M.Laughlin 的思路做进一步推广,以找到一些待解决的等幂和问题的突破口?为了深刻理解拉马努金、Hirschhorn 和J.M.Laughlin 等人的思路,我尝试先依照他们的方法,找出类似的新公式。 【五次方等幂和问题的新公式】 基于与 J.M.Laughlin 的文章所选用的同一组“两参数二次方公式解”,但我选用不同的特征方程(Characteristic Equation):J.M.Laughlin选的是 m_k^2-10 m_k n_k+n_k^2 所对应的 x^2 10x + 1 = 0 , 而我选择了 m_k^2-30 m_k n_k+n_k^2 所对应的 x^2 30x + 1 = 0,可得到以下五次方等幂和问题的新公式:若 \frac{x^2+484 x+3}{x^3-899 x^2+899 x-1}=:\sum_{n=0}^\infty a_n x^n,\frac{ - 5 x^2+ 418 x+3 }{x^3-899 x^2+899 x-1}=:\sum_{n=0}^\infty p_n x^n \frac{- 7 x^2 + 414 x +1}{x^3-899 x^2+899 x-1}=:\sum_{n=0}^\infty b_n x^n,\frac{3 x^2+724 x+1}{x^3-899 x^2+899 x-1}=:\sum_{n=0}^\infty q_n x^n \frac{-1}{x-1}=:\sum_{n=0}^\infty c_n x^n,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{- x^2+298 x-1}{x^3-899 x^2+899 x-1}=:\sum_{n=0}^\infty r_n x^n \frac{- 5 x^2 +708 x -7}{x^3-899 x^2+899 x-1}=:\sum_{n=0}^\infty d_n x^n,\frac{ x^2+774 x-7}{x^3-899 x^2+899 x-1}=:\sum_{n=0}^\infty s_n x^n \frac{3 x^2 +778 x -5}{x^3-899 x^2+899 x-1}=:\sum_{n=0}^\infty e_n x^n,\frac{-7 x^2+468 x-5}{x^3-899 x^2+899 x-1}=:\sum_{n=0}^\infty t_n x^n \frac{- 3 x^2 + 294 x -3}{x^3-899 x^2+899 x-1}=:\sum_{n=0}^\infty f_n x^n,\frac{-3 x^2+894 x-3}{x^3-899 x^2+899 x-1}=:\sum_{n=0}^\infty u_n x^n 则对于 1\leq j \leq 5 及 k\geq0 均有 a_k^j+ b_k^j+c_k^j+d_k^j+ e_k^j+ f_k^j =p_k^j+ q_k^j+ r_k^j+ s_k^j+ t_k^j+u_k^j , 或 p_k^j+ q_k^j+ r_k^j+ s_k^j+ t_k^j+u_k^j-a_k^j- b_k^j- d_k^j- e_k^j- f_k^j=c_k^j=1^j 例如,当 0 \leq\ n \leq 4 时,具体的数值是: a_{n}=-3, -3181, -2857023, -2565603961, -2303909500443 b_{n}=-1, -1313, -1179481, -1059173033, -951136204561 c_{n}=1, 1, 1, 1, 1 d_{n}=7, 5585, 5014627, 4503128765, 4043804615647 e_{n}=5, 3717, 3337085, 2996697837, 2691031319765 f_{n}=3, 2403, 2157603, 1937524803, 1739895115203 p_{n}=-3, -3115, -2797683, -2512316635, -2256057540963 q_{n}=-1, -1623, -1458181, -1309445643, -1175880729961 r_{n}=1, 601, 539401, 484381201, 434973778801 s_{n}=7, 5519, 4955287, 4449841439, 3995952656167 t_{n}=5, 4027, 3615785, 3246970447, 2915775845165 u_{n}=3, 1803, 1618203, 1453143603, 1304921336403 (-3181)^j + (-1313)^j + 1^j + 5585^j + 3717^j + 2403^j \\= (-3115)^j + (-1623)^j + 601^j + 5519^j + 4027^j + 1803^j \\(j=1,2,3,4,5) 【八次方等幂和问题的相关公式】 首先,我从现有文献中,找了以下一组“两参数二次方公式解”: a'_k=4 m_k n_k+m_k^2-6 n_k^2, \ \ \ p'_k=-18 m_k n_k+15 m_k^2-6 n_k^2 b'_k=-8 m_k n_k+11 m_k^2-10 n_k^2,\ \ \ q'_k=20 m_k n_k-15 m_k^2-10 n_k^2 d'_k=20 m_k n_k+5 m_k^2-30 n_k^2,\ \ \ s'_k=42 m_k n_k-9 m_k^2-30 n_k^2 e'_k=36 m_k n_k-11 m_k^2-34 n_k^2,\ \ \ t'_k=30 m_k n_k+m_k^2-34 n_k^2 容易证明,上述参数解满足: \left(a'\right)_k^j+\left(b'\right)_k^j+\left(c'\right)_k^j+\left(d'\right)_k^j+\left(e'\right)_k^j=\left(p'\right)_k^j+\left(q'\right)_k^j+\left(r'\right)_k^j+\left(s'\right)_k^j+\left(t'\right)_k^j\\(j=1,3,5,7) \frac{1}{6 x+1}=:\sum_{n=0}^\infty a_n x^n,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{3 \left(12 x^2-8 x+5\right)}{216 x^3-132 x^2-22 x+1}=:\sum_{n=0}^\infty p_n x^n \frac{60 x^2-44 x+11}{216 x^3-132 x^2-22 x+1}=:\sum_{n=0}^\infty b_n x^n,\frac{15 \left(4 x^2-1\right)}{216 x^3-132 x^2-22 x+1}=:\sum_{n=0}^\infty q_n x^n \frac{156 x^2-124 x-5}{216 x^3-132 x^2-22 x+1}=:\sum_{n=0}^\infty c_n x^n,\frac{3 \left(52 x^2-40 x+3\right)}{216 x^3-132 x^2-22 x+1}=:\sum_{n=0}^\infty r_n x^n \frac{5}{6 x+1}=:\sum_{n=0}^\infty d_n x^n,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{9 \left(20 x^2-16 x-1\right)}{216 x^3-132 x^2-22 x+1}=:\sum_{n=0}^\infty s_n x^n \frac{204 x^2-112 x-11}{216 x^3-132 x^2-22 x+1}=:\sum_{n=0}^\infty e_n x^n,\frac{204 x^2-160 x+1}{216 x^3-132 x^2-22 x+1}=:\sum_{n=0}^\infty t_n x^n 则对于 j=1,3,5,7 及 k\geq0 均有 a_k^j+ b_k^j+c_k^j+d_k^j+ e_k^j =p_k^j+ q_k^j+ r_k^j+ s_k^j+ t_k^j , 或 p_k^j+ q_k^j+ r_k^j+ s_k^j+ t_k^j- b_k^j- c_k^j- e_k^j=a_k^j+d_k^j=((-6)^k)^j+(5(-6)^k)^j 例如,当 0 \leq\ n \leq 4 时,具体的数值是: a_{n}=1, -6, 36, -216, 1296 b_{n}=11, 198, 5868, 152856, 4094640 c_{n}=-5, -234, -5652, -154152, -4086864 d_{n}=5, -30, 180, -1080, 6480 e_{n}=-11, -354, -9036, -243144, -6465456 p_{n}=15, 306, 8748, 229608, 6140016 q_{n}=-15, -330, -9180, -242280, -6470640 r_{n}=9, 78, 3060, 75672, 2051856 s_{n}=-9, -342, -8532, -230904, -6132240 t_{n}=1, -138, -2700, -77832, -2038896 (-6)^j+198^j+(-234)^j+(-30)^j+(-354)^j\\=306^j+(-330)^j+78^j+(-342)^j+(-138)^j\\(j=1,3,5,7) 根据等幂和数组的基本性质,这个解可以进一步推出八次方等幂和的公式解(略)。 【小结】 通过推导上面两个新公式,我对拉马努金立方和公式及其推广有了较深入的理解:
|