|
在物理学中,Langevin方程是一个很重要的随机微分方程,描述了系统在受到确定性和波动(“随机”)力的组合时如何演化。Langevin方程中的因变量通常是集体(宏观)变量,与系统的其他(微观)变量相比变化缓慢。快速(微观)变量是朗之万方程随机性质的原因。 1.Brown运动 2.Langevin方程 1.Brown运动在显微镜下观察悬浮在液体中的微小颗粒,可以看见颗粒不停地进行着无规律运动。布朗颗粒是非常微小的宏观颗粒,其直径的典型大小为 10^{-7}m\sim10^{-6}m 。颗粒不断受到液体介质分子碰撞。在任一瞬间,一个颗粒受到介质分子从各方向的碰撞作用力一般说来是互不平衡的,颗粒就顺着净作用力的方向运动。由于分子运动的无规性,施加在颗粒上的净作用力涨落不定,力的方向与大小都是不断变化,颗粒就不停地进行着无规律运动。  无规律的分子运动 下面从扩散的观点研究布朗运动,不妨设流体中布朗粒子流密度(单位时间内通过单位截面的颗粒数)为 j(r,t) ,l粒子数密度为 n(r,t) ,由Fick's laws[1]可知 j(r,t)=-D\nabla n(r,t) (1) 其中D代表介质的扩散系数,由流体的连续性方程,即 \nabla \cdot j(r,t)+\frac{\partial n(r,t)}{\partial t}=0 (2) 将式(1)代入式(2)后,可获得 \nabla^2n(r,t)-\frac{1}{D}\frac{\partial n(r,t)}{\partial t}=0 (3) 设t=0时,颗粒均匀位于r=0处,即 n(r,0)=N\delta(r) 。扩散方程(3)在初始条件下的解为 n(r,t)=\frac{N}{(4\pi Dt)^{3/2}}e^{-\frac{r^2}{4Dt}} (4) 计算对于颗粒的统计特性,即 <r(t)>=0,<r^2(t)>=\frac{1}{N}\int_{-\infty}^{+\infty}r^2n(r,t)dr=2Dt 最初集聚在原点上的布朗粒子“系综”随着时间的增加而扩散出去,在任意时刻t它的扩展的性质和范围分别由(4)式和(5)式所给定。扩散过程(很明显,是不可逆的)为我们描绘了一幅关于系综内单粒子行为的非常好的图像。 然而,要记住的重要事情是,无论我们把注意力放在系综中的单个粒子身上,或是作为一个整体的系综来看,这个现象的最终根源在于布朗粒子受到流体中分子永不停息、或多或少是随机的碰撞。换句话说,这个现象的不可逆的特征归根到底是由于流体分子施加于布朗粒子上的随机涨落力所引起的。于是这就导致另一种系统的、广义的布朗运动理论,即Langevin方程。 为了简单起见,下面只考虑粒子的运动在一个水平方向的投影。 设粒子的质量为m,在时刻t粒子的坐标为 x(t) ,\mathscr{F}(t)是由于流体分子不停地碰撞对粒子的作用力 。 \mathscr{F}(t) 由两部分组成: (i).一个为“平均力”部分,它表示粒子所受的黏滞阻力 -\frac{v}{B} 或 -\alpha v ,其中B是系统的迁移率,即粒子由于受到单位“外”力作用所获得的漂移速度。由Stokes'law[2],可得 B=\frac{1}{\alpha}=\frac{1}{6\pi \eta a} (5) (ii).另一部分为涨落力 F(t) ,相当于分子对于静止的布朗粒子的碰撞净作用力,其平均值 <{F}(t)>=0 。 由牛顿第二定理可获得 m\frac{d^2}{dt^2}x=\mathscr{F}(t)+\mathscr{R}(t)=-\alpha \frac{d}{dt}x+F(t)+\mathscr{R}(t) (6) 方程式(6)称之为Langevin方程,其中 \mathscr{R}(t) 为此外可能存在的其他外力,例如电磁力。 由于积分关系式 \dot xx=\frac{1}{2}\frac{d}{dt}x^2 ,\ddot xx=\frac{1}{2}\frac{d^2}{dt^2}x^2-\dot x^2 (7) 把式(7)代入式(6),并且取该积的系综平均 \frac{m}{2}\frac{d}{dt}\left( \frac{d}{dt}\bar{x}^2 \right)-m\bar{\dot x^2}=-\frac{\alpha}{2}\frac{d}{dt}\bar{x^2}+\bar{Fx} (8) 涨落力 F(t) 与粒子的位置无关,因此 xF(t) 的平均值等于 x 的平均值与 F(t) 的平均值的乘积,即 \bar{xF}=\bar{x} \cdot\bar{F}=0 假设Maxwellian 分布成立,在粒子与介质达到热平衡的情况下,根据能量均分定理粒子在x方向的平均动能为 \frac{1}{2}m\bar{\dot x^2}=\frac{1}{2}kT (9) 其中k为玻尔兹曼常数,T为温度。并且将式(9)代入式(8),即 \frac{m}{2}\frac{d}{dt}\left( \frac{d\bar{x^2}}{dt} \right)+\frac{\alpha}{2}\frac{d\bar{x^2}}{dt}=kT (10) 不妨设 d\bar{x^2}/dt=u ,方程式(10)可以改写为 \frac{m}{2}\frac{du}{dt}+\frac{\alpha}{2}u=kT (11) 求解式(11),由于 \alpha/m 很小,整理可得 u=Ce^{-\alpha t/m}+\frac{2kT}{\alpha}=\frac{2kT}{\alpha} (12) 我们注意到,忽略了式(12)中的指数项,意味着忽略了布朗粒子的惯性的影响。 即 \bar{x^2}=\frac{2kT}{\alpha}t 对比与扩散角度描述的brown运动,可获得关系式 D=\frac{kT}{\alpha}=BkT (13) 式(13)为Einstein relation[3],可见介质黏滞的最终起因(以及扩散的起因)就在于流体分子不停地运动所引起的随机涨落力。 爱因斯坦、斯莫陆绰斯基和朗之万等发展的布朗运动理论,不仅正确地说明了布朗运动的本质,而且预言了布朗运动的一系列特性。这些预言得到皮兰实验的完全证实。布朗运动是当时能够以最直接的方式把分子运动显示出来的物理过程。这些研究对物质原子论的确立曾经起过重要的历史作用。布朗运动的研究为随机过程的研究开辟了道路。 2.Langevin方程对于式(6)整理,有 \frac{d}{dt}v=-\frac{v}{\tau}+L(t),\bar{L(t)}=0 (14) 两端同时积分,整理有 v(t)=v(0)e^{-t/\tau}+e^{-t/\tau}\int_{0}^{t}e^{u/\tau}L(u)du (15) 因此,粒子的漂移速度 v(t) 是一个与时间有关的涨落函数。考虑均方速度 <v^2(t)> (式16),即 <v^2(t)>=v^2(0)e^{-2t/\tau}+2e^{-2t/\tau}[v(0)\int_{0}^{t}e^{u/\tau}<L(u)>du]+e^{-2t/\tau}\int_{0}^{t}\int_{0}^{t}e^{(u_{1}+u_{2})/\tau}<L(u_{1})L(u_{2})>du_{1}du_{2} 由于 <L(t)>=0 ,则均方速度<v^2(t)>的第二项为零,其中不妨设第三项中的二重积分为 I ,即 I=\int_{0}^{t}\int_{0}^{t}e^{(u_{1}+u_{2})/\tau}<L(u_{1})L(u_{2})>du_{1}du_{2}=\int_{0}^{t}\int_{0}^{t}e^{(u_{1}+u_{2})/\tau}K(u_{2}-u_{1})du_{1}du_{2}  二重积分求解过程 将其结果代入式(16),整理可得 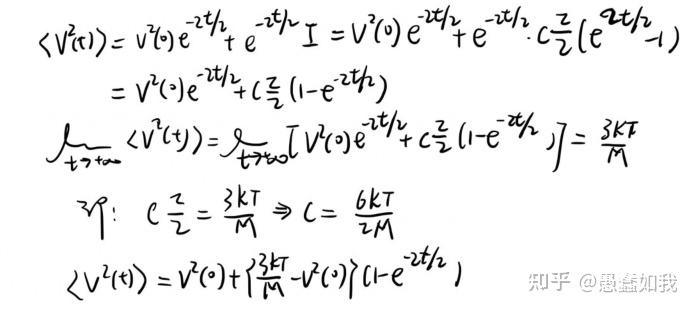 为了获得量 <r^2> 随时间t变化方式的典型描述,通过 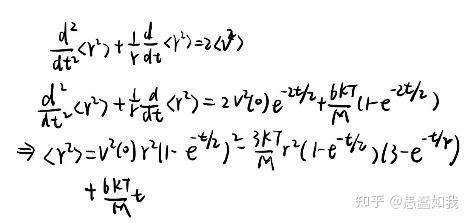 去布朗颗粒的数据[4] 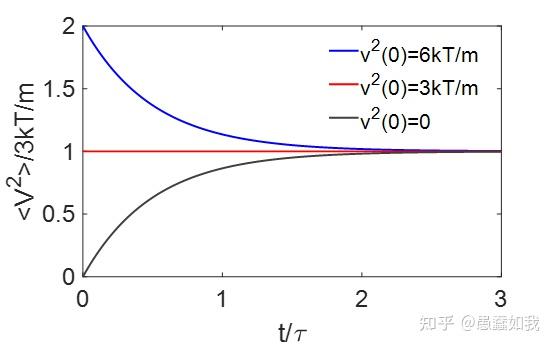 布朗粒子的均方速度与时间曲线 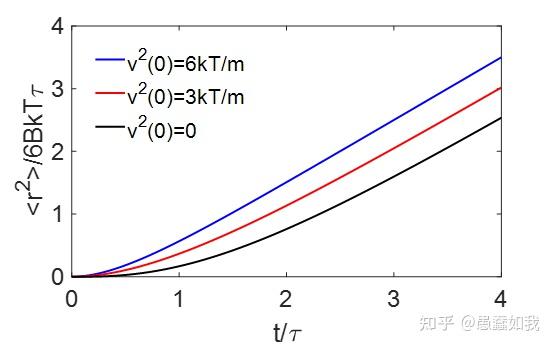 布朗粒子的均方位移与时间曲线 对于两者极限状态,通关分析有  1.对于 t\ll\tau ,粒子的运动具有可逆性,那时 <r^{2}>\simeq v^2(0)t^2 1.对于 t\gg\tau ,粒子的运动具有不可逆性,那时 <r^{2}>\simeq6BkTt=\frac{6kT\tau }{m}t 可见布朗运动具有耗散属性。 更多形式的Langevin 方程可见之后的分享。 参考
|