优化-拉格朗日乘子法

害，今天想看SVM，发现涉及到一个很重要的数学知识 --> 拉格朗日乘子法。我仿佛失忆了一样，完全还给我可爱的数学老师了，所以，看懂了之后，我来写一写吧。

拉格朗日乘子法：

• 拉格朗日乘子法（Lagrange multipliers）是一种寻找多元函数在一组约束下的极值的方法。
• 通过引入拉格朗日乘子，可将有 d 个变量与 k 个约束条件的最优化问题转化为具有 d+k 个变量的无约束优化问题求解。

举个例子：

• 求 f(x,y)=x^2+y^2 的最小值，约束条件是 g(x,y)=x+y+1=0 ，可以用下图表示。
• 这是一个等式约束，即约束条件是等式。当然约束条件也可以是不等式。
• 像这种需要在约束条件下求极值的问题，我们就可以用拉格朗日乘子法来做。

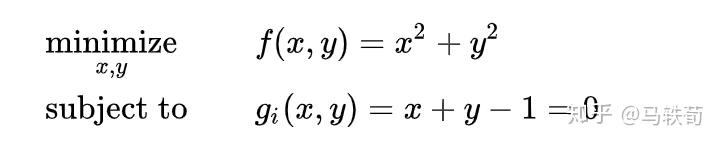等式约束：

当约束条件是等式的时候，例子：

• 求 f(\textbf x)=x_1^2+x_2^2 的最小值，约束条件： g(\textbf x) = x_1^2x_2-3=0
• minf(\textbf x)\ \ \ \ \ s.t. g(\textbf x)=0

直观操作步骤：

• 画出约束条件曲线 g(\textbf x) = x_1^2x_2-3=0
• 画出 f(\textbf x)=x_1^2+x_2^2 的等高线
• 找到 f(\textbf x) 和 g(\textbf x) 相交的点中的 f(\textbf x) 取得最小值的点（相切的位置），输出此时的 f(\textbf x) 值。

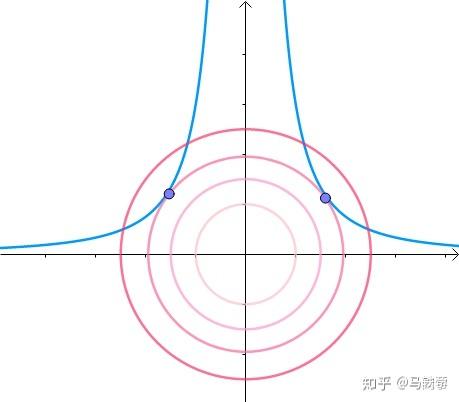那么，我们能得到什么信息呢？

• 约束曲线与极值曲线相切的点为极值点 \textbf x^* 。
• 对于约束曲面上的任意点 \textbf x ，该点的梯度 \nabla g(\textbf x) 正交于约束曲面。
• 在最优点 \textbf x^* ，目标函数在该点的梯度 \nabla f(\textbf x^*) 正交于约束曲面。

由此可知，在最优点 \textbf x^* ，梯度 \nabla g(\textbf x) 和 \nabla f(\textbf x) 的方向必相同或相反，即存在 \lambda \ne 0 ，使得： \nabla f(\textbf x^*) + \lambda\nabla g(\textbf x^*)=0 ， \lambda 称之为拉格朗日乘子。

所以在求解 f(x) 极值的问题上，我们相当于有两个条件了：

\begin{equation}\left\{\begin{array}{l} \nabla f(\textbf x) + \lambda\nabla g(\textbf x)=0 \\ g(\textbf x) = x_1^2x_2-3=0 \end{array}\right.\end{equation}

对于上面的具体例子，我们这两个条件，可联立方程： \begin{equation}\left\{\begin{array}{l} \nabla f(\textbf x)=\lambda \nabla g(\textbf x) \\ g(\textbf x)=x_1^{2} x_2-3=0 \end{array}\right.\end{equation} ，求解得到： \begin{equation}\left\{\begin{array}{l} \left(\begin{array}{c} 2 x_1 \\ 2 x_2 \end{array}\right)=\lambda\left(\begin{array}{c} 2 x_1 x_2 \\ x_1^{2} \end{array}\right) \\ x_1^{2} x_2-3=0 \end{array} \Longrightarrow\left\{\begin{array}{l} x_1 \approx \pm 1.61 \\ x_2 \approx 1.1 \\ \lambda \approx 0.87 \end{array}\right.\right.\end{equation}

上面的步骤就是用了拉格朗日乘子法进行求解的，最终求得了极值点。

仔细观察上面推出极值点的两个条件：

\begin{equation}\left\{\begin{array}{l} \nabla f(\textbf x) + \lambda\nabla g(\textbf x)=0 \\ g(\textbf x) =0 \end{array}\right.\end{equation}

• 他最简单的原函数是不是就是： f(\textbf x)+\lambda g(\textbf x) ，上面第一行是对 \textbf x 的求导等于0，第二行是对 \lambda 的求导等于0，哎呦，正合适哦是不是。
• 所以我们定义的拉格朗日函数为： L(\textbf x,\lambda)=f(x)+\lambda g(x)
• 将其对 \textbf x 的偏导数 \nabla _xL(\textbf x,\lambda) 置零，就得到 \nabla g(\textbf x^*) + \lambda\nabla f(\textbf x^*)=0
• 将其对 \lambda 的偏导数 \nabla _\lambda L(\textbf x,\lambda) 置零，就得到 g(x)=0
• 都对拉格朗日函数的偏导置零，能求出满足条件的极值点，说明什么？这tm就是在求 L(\textbf x,\lambda) 的极值点不是吗？？？哎呦我去，我是发现了什么了不起的大道理啊。

所以对 f(\textbf x) 在约束条件 g(\textbf x)=0 的求极值问题，是不是就转化成了对拉格朗日函数 L(\textbf x,\lambda) 的无约束优化问题啊。太棒了简直啊是不是。

所以呼应前面的定义：“通过引入拉格朗日乘子，可将有 d 个变量与 k 个约束条件的最优化问题转化为具有 d+k 个变量的无约束优化问题求解。”这句话突然都眉清目秀了起来是不是。

不等式约束：

当约束条件是不等式的时候，存在不等式约束时，最优解的位置只有两种情况，一种是最优解在不等式约束的边界上，另一种就是不等式约束的区域内，需要分为两种情况讨论。例子：

情况一：最优点在不等式约束的区域内

• 求 f(\textbf x)=x_1^2+x_2^2 的最小值，约束条件： g(\textbf x)=x_1+x_2-1\leq0
• minf(\textbf x)\ \ \ \ \ s.t. g(\textbf x)\leq0

直观操作步骤：

• 画出约束条件区域 g(\textbf x) = x_1+x_2-1\leq0
• 画出 f(\textbf x)=x_1^2+x_2^2 的等高线，其最小值为原点。
• 图如下，可以看到，这个不等式约束实际上包含了原点，所以这个约束等于没有。

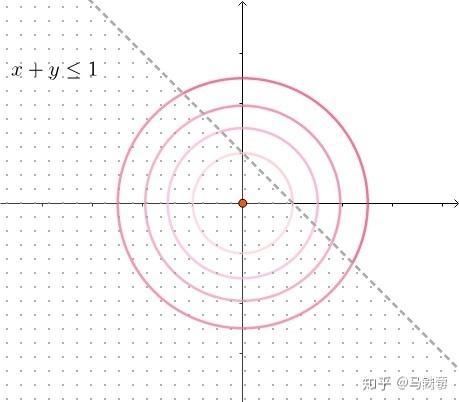抛开约束条件，按照正常求极值办法，直接对 f(\textbf x)=x_1^2+x_2^2 求梯度，令其等于0，即可得到极值点。 \nabla f(\textbf x)=0\Rightarrow(x_1,x_2)=(0,0)

情况二：最优点在不等式的边界上

• 求 f(\textbf x)=x_1^2+x_2^2 的最小值，约束条件： g(\textbf x)=x_1+x_2+2\leq0
• minf(\textbf x)\ \ \ \ \ s.t. g(\textbf x)\leq0

直观操作步骤：

• 画出约束条件区域 g(\textbf x) = x_1+x_2+2\leq0
• 画出 f(\textbf x)=x_1^2+x_2^2 的等高线，其最小值为原点。
• 图如下，可以看到，在不等式约束下，最优解是在边缘相切的地方取得，换句话说，最优解也在约束的边界上。

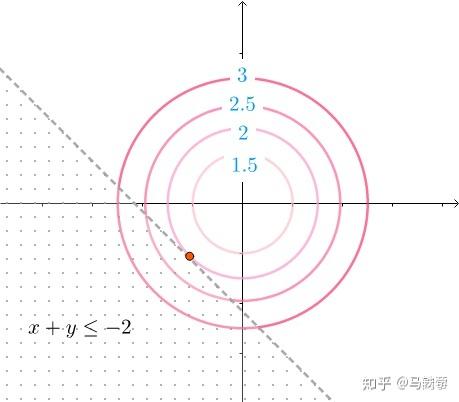在约束条件的边界上取得？稍等，这不就直接是等式约束了吗，相当于求 minf(\textbf x)\ \ \ \ \ s.t. g(\textbf x)=0 ，是不是这样呀。那就直接套上面拉格朗日乘子法的方法来求呗。

写出拉格朗日函数： L(\textbf x,\lambda)=f(\textbf x)+\lambda g(\textbf x)=x_1^2+x_2^2+\lambda(x_1+x_2+2) ， \lambda \ne 0 ，现在求约束条件下的极值问题就转换成求 L(\textbf x,\lambda) 的极值问题啦，所以令 \nabla _xL(\textbf x,\lambda)=0 和 \nabla _\lambda L(\textbf x,\lambda)=0 可求得最优解。

\begin{equation}\left\{\begin{array}{l} \nabla _xL(\textbf x,\lambda)=\nabla f(\textbf x)+\lambda \nabla g(\textbf x)=\left(\begin{array}{c} 2 x_1 \\ 2 x_2 \end{array}\right)+\lambda\left(\begin{array}{c} 1 \\ 1 \end{array}\right) =0\\ \nabla _\lambda L(\textbf x,\lambda)=g(\textbf x)=x_1+ x_2+2=0 \end{array} \Longrightarrow\left\{\begin{array}{l} x_1 = -1 \\ x_2 = -1 \\ \lambda = 0.5 \end{array}\right.\right.\end{equation}

两种情况合并：

那这两种情况，我们每次都需要分开讨论？？这不是很鸡肋吗，所以，让我们来找找规律，万一，有什么神奇的发现呢。

• 情况一：最优解在 g(\textbf x)<0 区域内，条件无作用，直接令 \nabla f(\textbf x)=0 求解。
• 这等价于将拉格朗日函数的 \lambda 置零，即 L(\textbf x,\lambda)=f(\textbf x)+\lambda g(\textbf x)=f(\textbf x) ，再对 L(\textbf x,\lambda) 求极值。
• 情况二：最优解在 g(\textbf x)=0 上，相当于等式约束，曲线相切处为最优解。
• 即满足 存在一个 \lambda 使得\nabla f(x^*) + \lambda\nabla g(x^*)=0 ，但是这里的 \lambda 的取值范围就不是不等于0了，这个时候最优解处 \nabla f(x^*) 的方向必须与 \nabla g(x^*) 的相反，即存在常数 \lambda>0 ，使得 \nabla f(x^*) + \lambda\nabla g(x^*)=0 。
• 整合情况：第一种 \lambda=0 ，第二种 g(\textbf x)=0 ，所以两种情况都满足 \lambda g(\textbf x)=0。
• 因此，在约束条件 g(\textbf x)\leq0 下最小化 f(\textbf x) ，可转化成在如下三个约束下最小化拉格朗日函数 L(\textbf x,\lambda)=f(\textbf x)+\lambda g(\textbf x) ：
• \begin{equation}\left\{\begin{array}{l} g(\textbf{x}) \leqslant 0 \\ \lambda \geqslant 0 \\ \lambda g(\textbf x)=0 \end{array}\right.\end{equation} ，这个式子成为 Karush-Kuhn-Tucker(KKT) 条件。

至于这个KKT，先留着吧，我就得到这里可能就够我看SVM的了？

拉格朗日乘子法总结：

就是求在约束条件下的极值问题的一种方法，把约束条件下求极值问题转化为求拉格朗日函数的极值问题。

参考：

• 非线性优化中的 KKT 条件该如何理解？
• 周志华老师的西瓜书

害，请问学习了拉格朗日乘子法的我，明天有资格手撕SVM了吗？？？