数值分析(8)：数值积分之Lagrange法

更多数值分析内容，欢迎关注笔者@ReEchooo

同时也可以关注以下数值分析专栏：

1. 引言

在做定积分时，如果能够求出被积函数的原函数，那么定积分很容易求出，但是在工程中遇到的定积分大多数是求不出原函数的，那么如何用一些手段来估计这个定积分使得结果满足一定的精度呢？

解决问题的基本方法是用 插值多项式 近似 被积函数 f(x) 把 插值多项式的积分值 作为原积分的近似值。

在正式介绍求积公式之前，首先来回顾三个知识点，分别是 积分中值定理 ， Lagrange插值多项式 ， 均差 。

2. 数值求积基本原理

如果用n次Lagrange插值多项式近似被积函数，那么有估计积分值为：

因为Lagrange插值多项式估计被积函数就有误差，那么积分后自然也有误差， 求积误差 定义为：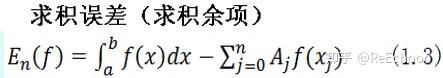

3. 两个简单的求积公式

3.1 梯形公式

所谓梯形公式，直观来看即为下图所示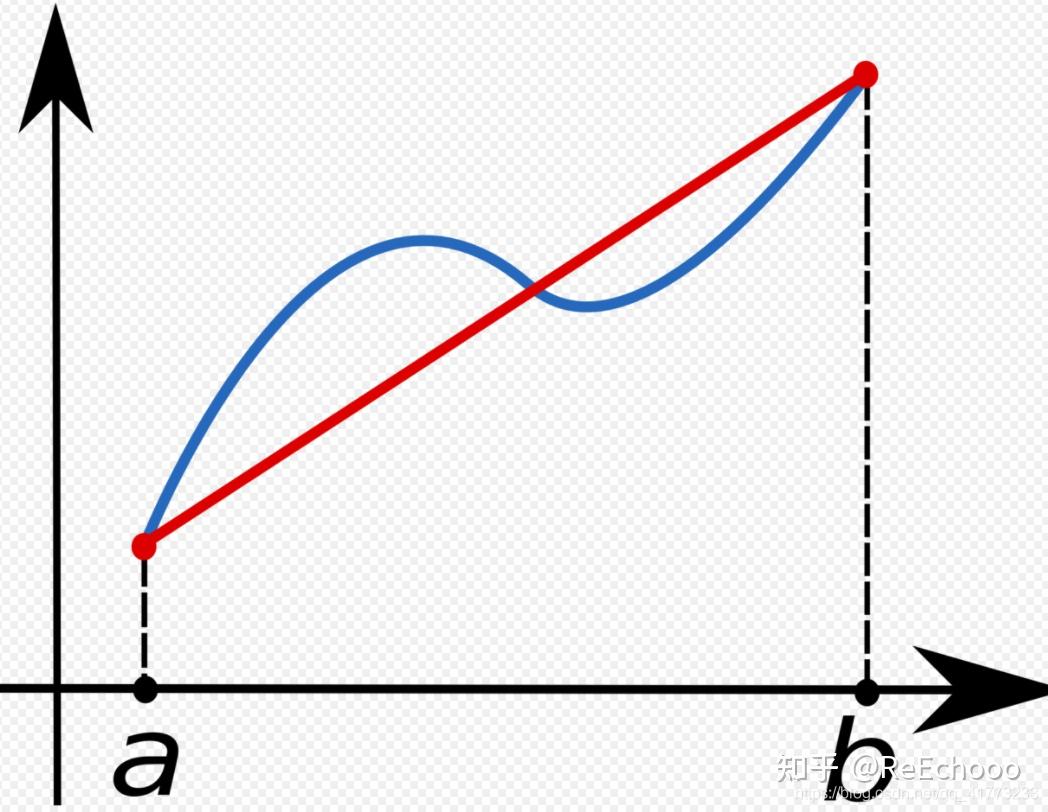

这可以用一次Lagrange插值多项式近似，推导过程如下，推导后能够得到梯形公式：

接着对 插值余项积分 即可得到 求积余项 ，梯形公式的求积余项推导如下：

3.2 Simpson求积公式

显然梯形公式是不够精确的，如果用 二次Lagrange插值多项式 来近似被积函数，那么会得到更加精确的结果。此时的求积公式为 Simpson求积公式

假设二次Lagrange插值多项式所使用的插值节点是两个区间端点以及区间的中点，那么 Simpson求积公式 推导如下：

同理，Simpson求积公式的求积余项为：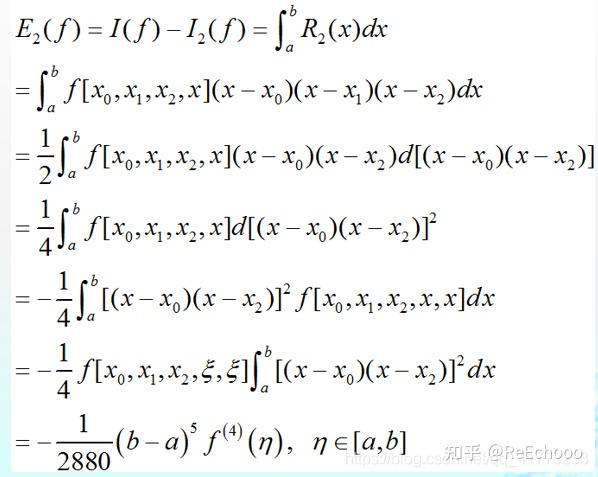

注意这个求积余项的角标为2，而梯形公式的求积余项角标为1，显然这个角标代表的含义是lagrange插值多项式的次数。

4. 代数精度

为了刻画用Lagrange插值多项式近似求积的精度，定义 代数精度 ：

梯形公式 的 求积余项 是一个含 二阶导 的数，那么显然对于任何一次函数及零次函数的求积余项均为0，对于二次函数的求积余项不为0，故具有1次代数精度。 Simpson求积公式 的 求积余项 是一个含 四阶导 的数，那么显然对于任何三次函数及其以下次数函数求积余项均为0，对于四次函数的求积余项不为0，故具有3次代数精度。即：

根据求积余项具备线性性，即：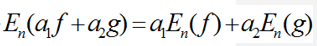

可知（1.2）式的等价定义为：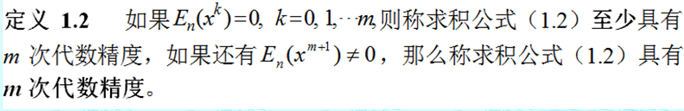

5. 插值型求积公式

前面的梯形公式和Simpson公式只是用特殊的Lagrange插值多项式进行近似，很自然地，我们可以将其推广到n阶Lagrange插值多项式，即得到所谓的 插值型求积公式 ：

因为 l_j(x) 只与插值节点有关，所以 A_j 也就只与插值节点有关，而与函数 f(x) 无关。 因为所有 l_j(x) 的和为1，所以所有 A_j 的和为(b-a)

关于 插值型求积公式 的 代数精度 ，有如下定理

参考文献：

关治，陆金甫《数值方法》