多元函数微分学条件极值(拉格朗日乘数法)求解技巧总结

看到多元函数条件极值的题目，常用拉格朗日乘数法对号入座。但有时候如坐针毡，因为这种看似万能的方法计算量太大了。解方程解的生无可恋是常态。所以我总结了一些解条件极值的小技巧，希望对大家有所帮助。

总的来说，思路分为五种：

1.从前几个式子中找出 x,y,z 之间的关系，然后带入到 \varphi (x,y,z)=0 中解出来；
2.先求出\lambda 的值，化简式子。
3.目标函数的极值可以用 \lambda 表示，然后只用求 \lambda 即可；
4.转换目标函数，使拉氏函数变的简单。
5.降维转变为一元函数求极值。
以下八种技巧都是围绕上面五点进行展开的。
(文末彩蛋：利用不等式解最值)

技巧一：硬核作差法

先用二元函数举例来说明此技巧：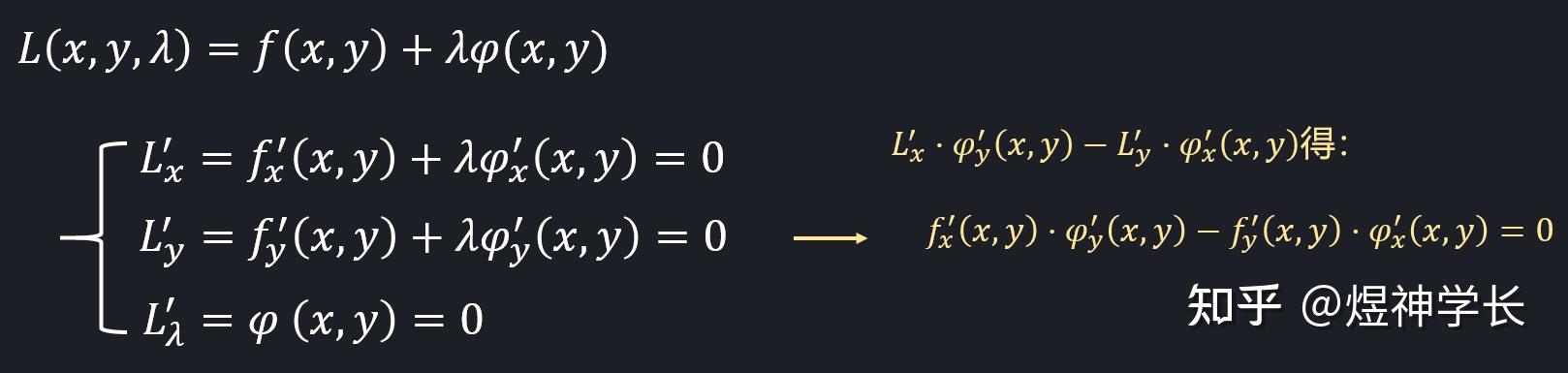

这个方法可以去除\lambda，进而转变为不含\lambda的式子，再与 \varphi(x,y)=0 配合（两个方程，两个未知数），从而解出 x,y 。例题如下所示：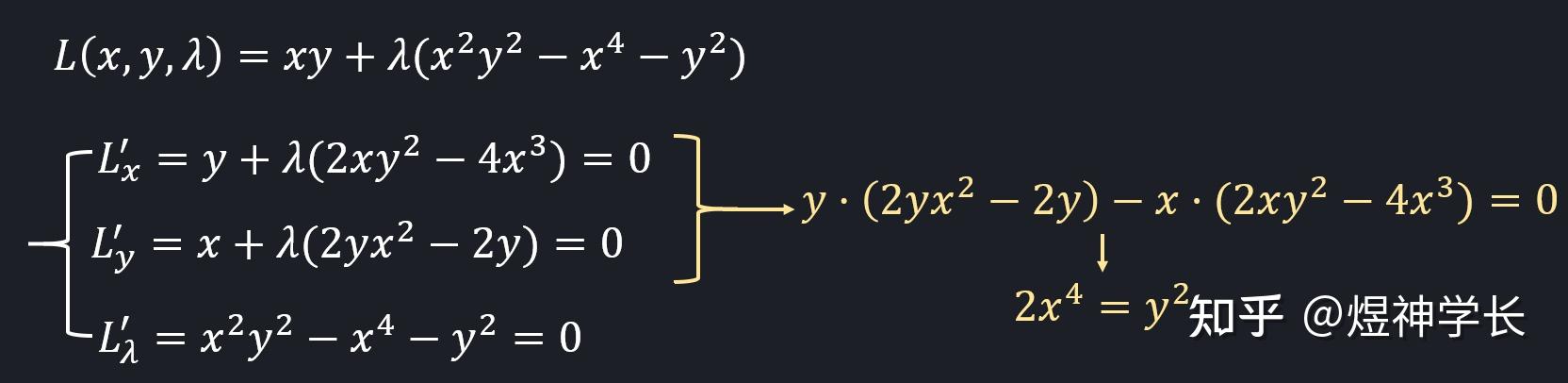

通过该方法，可以轻松得到 x,y 之间的关系，此时再带入到 x^{2}y^{2}-x^{4}-y^{2}=0 中，即可解出对应的 x,y 。

对于三元函数类似，只不过这时候要作差两次，如下例题：

此时作差了两次，这里需要注意作差的式子要灵活选择，选取不当会导致计算量增大。

比如本题如果选择： L_{x}^{'}\varphi_{y}^{'}-L_{y}^{'}\varphi_{x}^{'} 和L_{y}^{'}\varphi_{z}^{'}-L_{z}^{'}\varphi_{y}^{'} 则不容易解出来。

另外需要注意这种解法不会漏解，但是有可能会增解。例如本题 x=\pm\sqrt{10}，y=z=0 就是多出来的解。

技巧二：单项连等法：

目标函数是 f(x,y,z)=mx^{a}y^{b}z^{c} 时（ m,a,b,c 均不为0），可以尝试使用。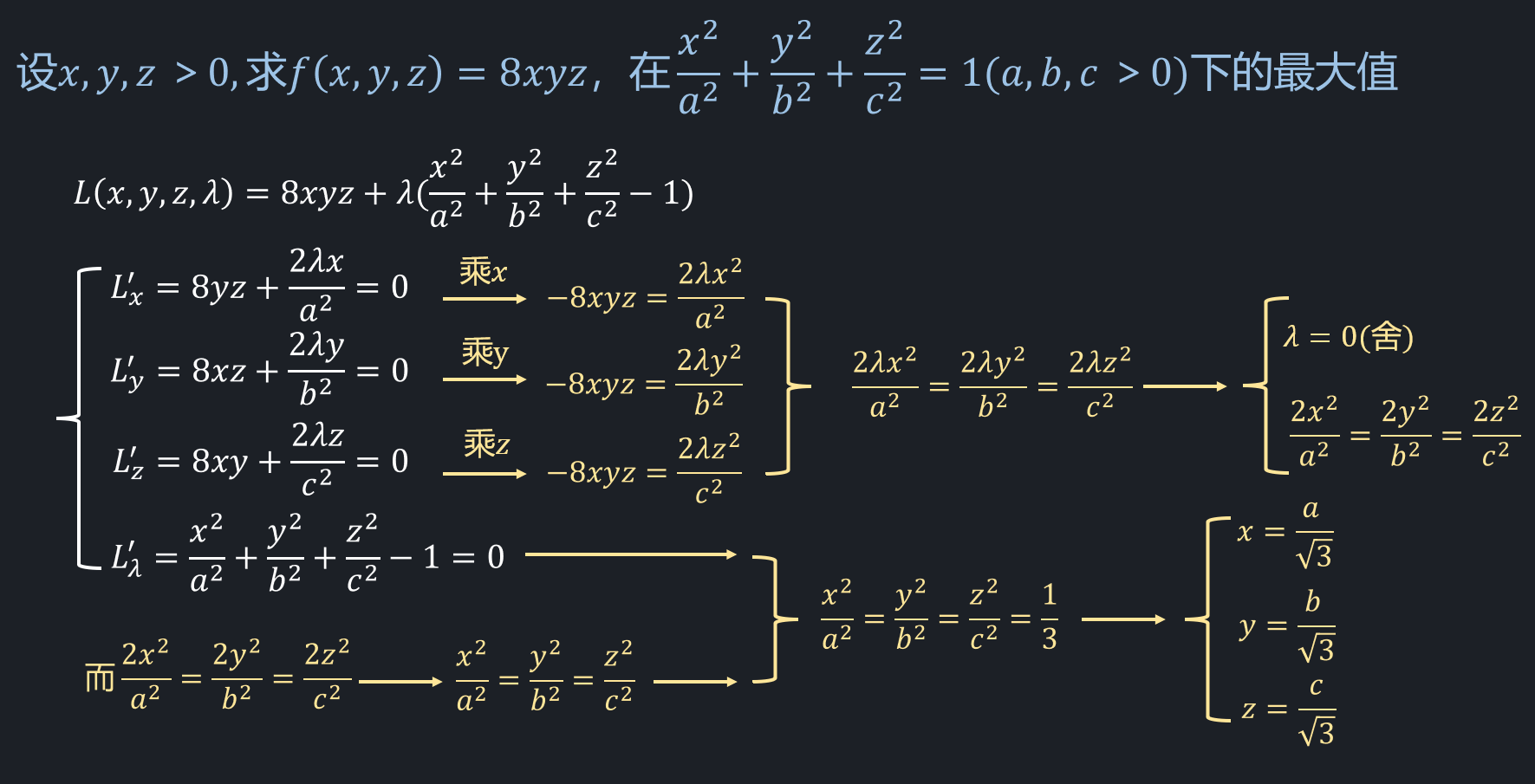

就是构造出相等的项，将其放在等号一边之后连等就可以了。该方法可以通过讨论消除 \lambda ，进而变成不含\lambda 的连等式或直接得到\lambda =0 。其中本题的连等式可以写成两个等式，因此本题也可以看成是变成了三个方程三个未知数的形式。

即：1. \frac{x^{2}}{a^{2}}=\frac{y^{2}}{b^{2}} ;2. \frac{y^{2}}{b^{2}}=\frac{z^{2}}{c^{2}} ;3. \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}-1=0

技巧三：对称作差法：

目标函数 f 和约束条件中的 \varphi 关于 y=x 或 z=x 对称，则可以考虑使用。

函数关于 y=x 对称，就是互换函数中的 x 和 y 表达式不变。关于 z=x 对称同理。

技巧简述：

1. f(x,y,z) 和\varphi(x,y,z)关于 y=x对称：

我们需要做的是让 L_{x}^{'}=0 减去 L_{y}^{'}=0 ，得到的式子可以变形成： (y-x)(整式)=0 ，从而简化计算。同时如果其中有 y≠x 的解，则将它的 x，y 互换后则是另一个解。

例如： (x,y,z)=(a,b,c) 是其中一个解，那么 (x,y,z)=(b,a,c) 一定也是另一个解。

2.若f(x,y,z) 和\varphi(x,y,z)关于 y=z 对称：

则让 L_{y}^{'}=0 减去 L_{z}^{'}=0 ，得到的式子可以变形成： (y-z)(整式)=0 。同时如果其中有 y≠z 的解，则将它的 y,z 互换后则是另一个解。

2.若f(x,y,z) 和\varphi(x,y,z)即关于 y=x 对称又关于 y=z 对称：

同时进行上面两个操作。

本题使用该技巧变形成了 (x-y)(2\lambda-z^{3})=0 ，但 2\lambda-z^{3}=0 是不成立的，因此可以得到 y=x 这个式子。这也是很多人所说的取巧的方法：若 f 和 \varphi 关于 y=x 对称，则就可以得到 y=x 这个式子。这个方法虽然有时候非常有效，但是有点像赌博，就是赌后面乘的那个式子不能为0。

当然，本题由于目标函数是 xyz^{3} ，因此直接用技巧二也能算出来，并且更简单，有兴趣的小伙伴可以自行做下。

技巧四：行列式求解法：

如果求出来的 L_{x}^{'}=0 , L_{y}^{'}=0 , L_{z}^{'}=0 组成的为线性方程组，则可以根据线性代数知识解决，以题为例，如下所示：

由于 x^{2}+y^{2}+z^{2}-10=0的存在，将导致 x,y,z 不可能同时为0，因此(1)~(3)式所组成的线性方程组一定有非0解，因此就是系数行列式为0，即可将 \lambda 解出，减少未知数的个数，进而容易求解。

技巧五：齐次构造法

如果目标函数 f 是齐次的，同时约束条件可以转化成齐次函数 g(x,y,z)=c 的形式。

齐次函数说白了，就是每一项中变量的指数和都相等。 比如： g(x,y)=x^{2}+y^{2}+xy 就是2次齐次函数

技巧简述：

若此时目标函数 f(x,y,z) 为m次齐次函数， g(x,y,z) 为n次齐次函数( m,n≠0 )，则可以构造出这个式子： f(x,y,z)=-\frac{cn}{m}\lambda 。此时再求出 \lambda 的值即可求出目标函数 f(x,y,z) 的最值。

所以该方法只需求 \lambda 即可，但是有时候 \lambda 并不好求。但有一种情况 \lambda 好求：求出来的 L_{x}^{'}=0 , L_{y}^{'}=0 , L_{z}^{'}=0 组成的为线性方程组时。因为这个时候可以用行列式解出 \lambda (技巧四)。

由此可见，在这种情况下，能够很快的求出我们的最值。但如果想要求最值点的话，就要麻烦一些了。

技巧六：目标函数转换法

如果可导函数 g(x) 在目标函数值域内是单调的。那么求目标函数的极值点可以转化为求 g(目标函数) 的极值点。

比如求f(x,y)= \sqrt{x^{2}+y^{2}} 在 \varphi(x,y)=0 下的极值点，可以转变为求 [f(x,y)]^{2}=x^{2}+y^{2} 在 \varphi(x,y)=0 下的极值点。其中 g(x)=x^{2} ，其可导且在 f(x,y) 值域内( [0,+\infty) )单调递增。

该技巧需要注意，求出来极值点后要带入到目标函数中得到极值，而不是带入到 g(目标函数) 中，这点需要注意。

本题也可以设 g(x)=\frac{1}{x} ，此时可以转变为求 xyz 的极值点即可。

技巧七：带入降维法：

把约束条件\varphi(x,y)=0看成一个隐函数，如果这个隐函数可以显化，则可以将显化后的函数带入到目标函数中，进而可以"降维"成一元函数，从而利用一元函数知识求极值（求导，单调性）。

技巧八：参数降维法：

若约束条件中的 \varphi(x,y)=0 ，可以转变成形如： ax^{2}+by^{2}=1 (其中a,b大于0)，则可以设 x=\frac{cos\theta}{\sqrt{a}} , y=\frac{sin\theta}{\sqrt{b}} ，再带入到目标函数中，继而解决问题。

彩蛋技巧：不等式求解法

数学基础比较好的可以了解此方法：

就是直接用不等式解决最值问题，简单粗暴。这里以上面题型四和题型七为例，看一下本方法。

题型四不等式解法：

题型七不等式解法：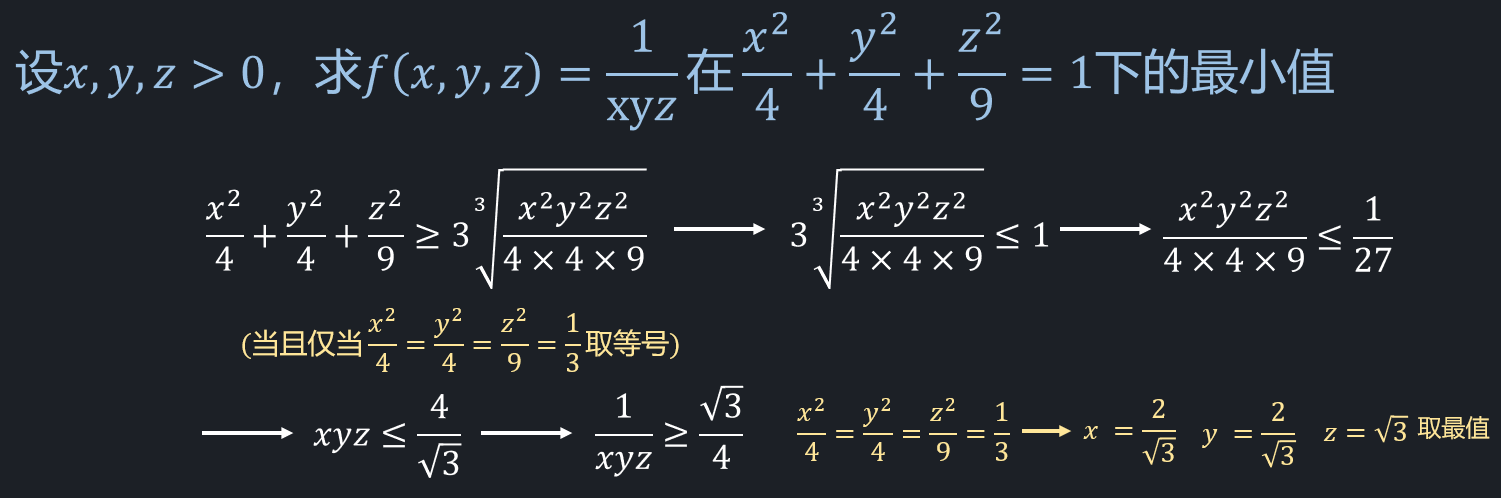

到这里方法基本就讲完了，但是我还想补充几点：

1.技巧是死的，人是活的，在解题中要灵活的运用技巧。选择合适的技巧和方法尤为重要，而如何合适选择，则要根据自己的经验来确定。因此如果这块比较薄弱，那么建议多做这块的题，然后结合本篇文章再进行归纳和总结，生成自己的经验与技巧。

2.解题时，有可能会出现增解的情况，例如技巧一中的情况。所以平时解出极值点之后，建议再带点到每个方程中演算一下。这样也能检查自己的结果是否正确，是一个比较好的习惯。

3.暑假接近尾声。后半程的复习，就不光是要求速度，还要要求质量，做好针对基础和题目的查漏补缺工作，才是解题能力提升的最坚实阶梯。

我是煜神学长，22考研我们一起加油！！！

往期总结笔记：

煜神学长：148分学长考研数学结论总结（秒杀函数、极限与连续-第1期）

煜神学长：148分学长考研数学结论总结（秒杀函数、极限与连续-第2期）

煜神学长：148分学长考研数学结论笔记-导数与微分解题技巧（第3期）

煜神学长：148分学长考研数学结论笔记-一元函数积分学解题技巧总结（第四期）

煜神学长：148分学长考研数学结论笔记-多元函数微分学解题技巧总结（第五期）

其他干货文章：

煜神学长：正交变换最强总结笔记，解决每一个考研线代人的理解难关

煜神学长：超强换元法，二重积分计算的核武器！（雅可比行列式超通俗讲解）

煜神学长：高数极限概念题，90%的人都会做错的一道题

煜神学长：考研秘技-拉格朗日中值定理横扫极限难题！(秒杀5种题型)

煜神学长：一文搞懂考研数列极限问题(概念/计算/证明)史上最强/最全总结！！

我和另一位学长做的数学强化轮-真题轮提分利器（思维导图）：