|
自己一直用史济怀老师的视频和教材学习数学分析。对于史济怀老师证明拉格朗日中值定理的方法感觉太突兀了,在看知乎关于史济怀老师那本书的评论时,甚至有人因为一个定理的证明就否定整本书,我觉得还是欠妥,我个人认为,史济怀老师的书以及讲课视频还是挺不错的。 下面步入正题。证明过程一般是用费马定理先证明罗尔定理,再根据罗尔定理证明拉格朗日中值定理。史济怀老师直接构造了一个函数,显得很突兀。我认为证明思路如下是比较好的(具体细节,如闭区间连续,开区间可导之类的话不再赘述): 根据罗尔定理,如果R上的函数 f(x) 满足以下条件:f(a)=f(b),则至少存在一个 ξ∈(a,b),使得 f'(ξ)=0。 再看拉格朗日中值定理形式 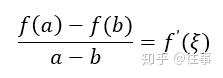 为了证明,我们先变换一下 f(a)-f(b)=f'(\xi)(a-b) …………………………式1 f(a)-f(b)-f'(\xi)(a-b)=0 …………………式2 结合罗尔定理,我们很自然联想到式2左边是某个函数的导数就好了。因此可以很容易联想到下面的函数: g(x)=(f(a)-f(b))x-f(x)(a-b) …………式3 很容易验证,式3的导数就是式2左边部分,且 g(a)=g(b)=bf(a)-af(b) …………式4 根据罗尔定理存在 ξ∈(a,b)使得 g'(\xi)=0 , 即式2成立,由此,拉格朗日中值定理得证。 同样的思路也可以用在柯西(Cauthy)中值定理证明。 |